平衡二分木の世界では近年では赤黒木(Red-Black Tree, RB-tree)が標準的である。追加、検索、削除がそれぞれ最悪O(log N)というすぐれものだが、場合分けが多く実装はけっこう面倒だ。
赤黒木というのはB木(Balanced tree)の一種である2-3木/2-3-4木をベースにした平衡二分木で、ノード内のリンクを赤、ノード外とのリンクを黒とラベル付けし、赤リンクの数が黒リンクの数を上回らず、黒リンクのみを数えた高さで見て平衡、つまりlog Nの高さを保証したというもの。つまり赤リンクを含めても2*log N以下に必ず納まるのだ。詳しく知りたければ調べてください。
昨年にRobert Sedgewick氏によって発表されたLLRBツリー(Left-Leaning Red-Black Tree)というのは、2-3木/2-3-4木を2分木に表現した赤黒木の赤リンクの形式に制約をかけ(左寄せする＝Left-Leaning)、一意になるようにして場合分けを少なくし、実装しやすくした赤黒木の改良版だ。赤黒木に対して性能が上がるということはないが、実装のしやすさは格段に向上しているという触れ込み。実際、Javaのソースで200行を切っており、この操作だけでパターンを網羅していることが理解できれば、かなり楽に実装できてしまう。
正直私は赤黒木を自力で実装するのは難儀だと思っていたので、LLRBの出現はまさに渡りに船だった。
会社で使おうと思ってC言語で実装(作業自体はコピペに近い)してみたのだが、なぜかdeleteがうまく動かなかった。そのときはもう少し複雑なdeleteのソースを探してきたものを移植して使ったのだが、ちょっと納得できないので自宅で元のサンプルソースから再実装してみたところ、deleteも正しく動いた。インタフェースを少しいじって(自分では使いやすくしたつもり)、公開しておく。ヘッダとソース、テストコードを合わせて381行(内テストコードが100行くらい)というサイズだ。イテレータは未実装だが、会社で作った「スタックを持ったイテレータ」を書くか、親リンクの処理を書いてnextをたどれるようにするかで迷っているところ。どっちが楽かな。
ついでに、STLのmapも内部では赤黒木を使っているのだが、性能を比較してみた。STLの場合はテンプレートだから比較関数がインライン展開できたり、性能チューニングもかなり入っているので、サンプルソースを元にした再帰使いすぎの実装より性能が高いのは当然だが、比較して見るとまあ、それほどひどい差ではないかなぁと思う。VMware上のLinuxで測定したので正確な測定ではないですが。
- stlmap-test.C
- SConstruct (sconsでコンパイルすると実行ファイルができます)
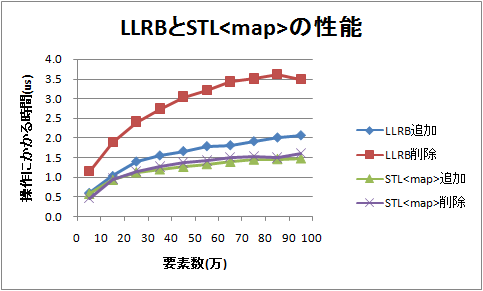
サンプルソースでは削除時にエントリがない場合の処理が考慮されておらず、そのままではSEGVを受けてしまうため、一度検索して存在を確認したあとにdeleteを実行している。そのため実行時間が倍近くかかっているが、エントリが存在しない場合のコードをdeleteの中に書くだけでもう少し速くなると思う。